Mastering Mathematical Thinking

What does it mean to “think like a mathematician”? Math is much more than following rote processes and plugging numbers into equations. Math is a way of looking at and thinking about our world. When students understand the “why” and “how” behind the math they are learning, they become flexible, intuitive problem solvers. 

But mathematical thinking isn’t something that comes naturally to most of us. It needs to be specifically taught, nurtured and developed. To be successful with higher math, students need to develop deep cognitive structures for problem solving and mathematical thinking. Thinking Maps give students a structure for thinking mathematically and explaining their reasoning.

Want to know more? Join our upcoming webinar: Building Deep Structures for Mathematical Thinking.

Mathematical Reasoning: Thinking Like a Mathematician

Math is an activity with a very high cognitive load. Students need to be able to follow processes and instructions, juggle all of the information provided in the problem, and recall prior knowledge and skills. Math also requires significant reading comprehension skills to understand directions or deconstruct a word problem. 

One of the biggest problems many students have in math is simply knowing where to start and what kind of thinking is required. Math involves many different types of cognition: comparing, classifying, generating ideas and solutions, following processes, if…then thinking, and decomposing numbers, shapes, or formulas, to name a few.

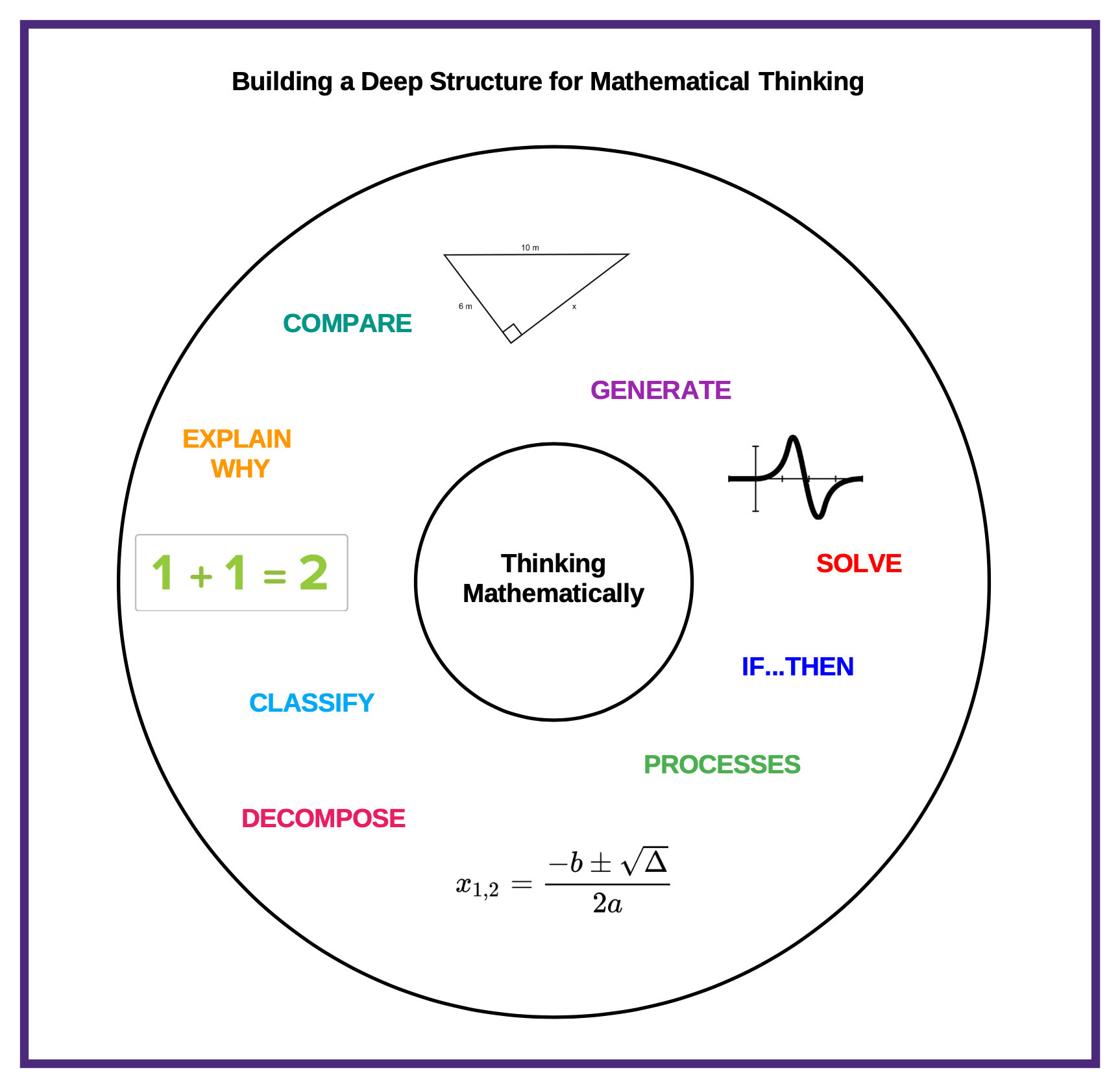
Mathematicians know how to apply and combine these types of thinking flexibly to solve many different types of problems. Visual Thinking Maps help students activate the right kinds of thinking for the problem at hand. For example, consider the problem of finding the surface area of a rectangular prism. Where do you start? What kind of thinking is required? 

One way to tackle this type of problem is with “part-to-whole” thinking. A rectangular prism has 6 flat surfaces: 4 sides and 2 ends. If I know how to find the area of a rectangle, I can calculate the area of each surface individually and then add them together to get the whole area. We can show this thinking in a Brace Map like this:

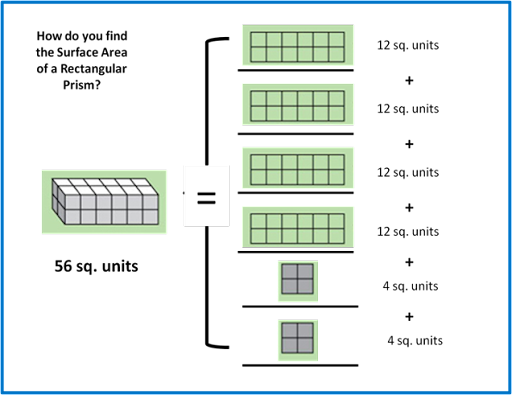
Now, the problem isn’t so intimidating. I just add up the parts to get the whole! This is an example of decomposing to solve a problem. 

Or suppose students need to find equivalent decimals and fractions. How is a decimal related to a fraction? A Bridge Map is a great way to show this relationship, using the relating factor “is equivalent to.”

Let’s Talk Math: Mathematical Discourse

Today’s math standards and assessments require students to do more than just come up with the right answer. Students need to be able to explain their thinking, either orally, visually or in writing. Mathematical discourse is an important skill in its own right and a critical part of developing mathematical thinking. When students go through the process of explaining their answers, they are cementing their knowledge, exposing and filling knowledge gaps, and deepening their understanding of the “how” and “why” of mathematical problem solving. 

Consider this word problem: 

I put a number in a bag. It is between 15 and 20. It is an even number. It is not 18. What number is it?

How do we start this problem? Students could just guess, but a systematic approach helps them get to the answer faster—and builds problem-solving skills they can apply to more complex problems later. This Flow Map helps students explain their thinking as they come up with the right answer.

The Map is a great visual representation of their thinking process. They can also easily take information back off the Map to explain their process in writing. This kind of exercise is a great way to help students prepare for state assessments that require them to explain their thinking in writing.

Reducing the Cognitive Load of Math

When students have a clear structure for approaching problem solving, the cognitive load of math is significantly reduced. Students in a Thinking Maps school learn how to use the Maps in a variety of ways to build mathematical knowledge, skills and reasoning. For example, students learn to use the Maps to:

• Use “signal words” like take apart, leads to, is the same as, or types of to activate the right kind of thinking for a problem. 
• Define mathematical terms and gather prior knowledge.  
• Explain and follow the steps in mathematical processes. 
• Deconstruct word problems for easier problem solving. 
• Compare and classify related concepts, equations, shapes or numbers. 
• Decompose shapes, equations or sets into their constituent parts. 
• Solve a variety of problem types using “if…then” thinking. 
• Visualize mathematical relationships. 

Using visual Maps makes mathematical thinking concrete and visible. Students are now equipped with a variety of tools to tackle all kinds of problems—so instead of staying stuck when they reach a problem they don’t know how to solve, they can start looking for clues that tell them which kind of thinking they should reach for. Over time, practicing these skills develops solid problem-solving habits and deep cognitive structures for mathematical thinking. 

Download the webinar to learn more.